3D Reconstruction
Goal
In this practice, the intention is to program the necessary logic to allow kobuki robot to generate a 3D reconstruction of the scene that it is receiving throughout its left and right cameras.

Instructions
This is the preferred way for running the exercise.
Installing and Launching
-
Download Docker. Windows users should choose WSL 2 backend Docker installation if possible, as it has better performance than Hyper-V.
-
Pull the current distribution of Robotics Academy Docker Image:
docker pull jderobot/robotics-academy:latest
-
In order to obtain optimal performance, Docker should be using multiple CPU cores. In case of Docker for Mac or Docker for Windows, the VM should be assigned a greater number of cores.
-
It is recommended to use the latest image. However, older distributions of RADI (Robotics-Academy Docker Image) can be found here.
How to perform the exercises?
-
Start a new docker container of the image and keep it running in the background:
docker run --rm -it -p 7164:7164 -p 2303:2303 -p 1905:1905 -p 8765:8765 -p 6080:6080 -p 1108:1108 -p 7163:7163 jderobot/robotics-academy -
On the local machine navigate to 127.0.0.1:7164/ in the browser and choose the desired exercise.
-
Wait for the Connect button to turn green and display “Connected”. Click on the “Launch” button and wait for some time until an alert appears with the message
Connection Establishedand button displays “Ready”. -
The exercise can be used after the alert.
Enable GPU Acceleration
- Follow the advanced launching instructions from here.
Where to insert the code?
In the launched webpage, type your code in the text editor,
from GUI import GUI
from HAL import HAL
# Enter sequential code!
while True:
# Enter iterative code!
Using the Interface
-
Control Buttons: The control buttons enable the control of the interface. Play button sends the code written by User to the Robot. Stop button stops the code that is currently running on the Robot. Save button saves the code on the local machine. Load button loads the code from the local machine. Reset button resets the simulation (primarily, the position of the robot).
-
Brain and GUI Frequency: This input shows the running frequency of the iterative part of the code (under the
while True:). A smaller value implies the code runs less number of times. A higher value implies the code runs a large number of times. The numerator is the one set as the Measured Frequency who is the one measured by the computer (a frequency of execution the computer is able to maintain despite the commanded one) and the input (denominator) is the Target Frequency which is the desired frequency by the student. The student should adjust the Target Frequency according to the Measured Frequency. -
RTF (Real Time Factor): The RTF defines how much real time passes with each step of simulation time. A RTF of 1 implies that simulation time is passing at the same speed as real time. The lower the value the slower the simulation will run, which will vary depending on the computer.
-
Pseudo Console: This shows the error messages related to the student’s code that is sent. In order to print certain debugging information on this console. The student can use the print() command in the Editor.
Robot API
from HAL import HAL- to import the HAL(Hardware Abstraction Layer) library class. This class contains the functions that sends and receives information to and from the Hardware(Gazebo).from GUI import GUI- to import the GUI(Graphical User Interface) library class. This class contains the functions used to view the debugging information, like image widgets.HAL.getImage('left')- to get the left imageHAL.getImage('right')- to get the right imageHAL.getCameraPosition('left')- to get the left camera position from ROS Driver CameraHAL.getCameraPosition('right')- to get the right camera position from ROS Driver CameraHAL.graficToOptical('left', point2d)- to transform the Image Coordinate System to the Camera SystemHAL.backproject('left', point2d)- to backprojects the 2D Image Point into 3D Point SpaceHAL.project('left', point3d)- to backprojects a 3D Point Space into the 2D Image PointHAL.opticalToGrafic('left', point2d)- to transform the Camera System to the Image Coordinate SystemHAL.project3DScene(point3d)- to transform 3D Point Space after triangulation to the 3D Point ViewerGUI.ShowNewPoints(points)- to plot a array of plots in the 3D visorGUI.ShowAllPoints(points)- to clear the 3D visor and plot new array of plotsGUI.ClearAllPoints()- to clear the 3D visorGUI.showImageMatching(x1, y1, x2, y2)- to plot the matching between two imagesGUI.showImages(imageLeft,imageRight,True)- allows you to view a debug images or with relevant information
def algorithm(self):
#GETTING THE IMAGES
# imageR = self.getImage('right')
# imageL = self.getImage('left')
#EXAMPLE OF HOW TO PLOT A RED COLORED POINT
# position = [1.0, 0.0, 0.0] X, Y, Z
# color = [1.0, 0.0, 0.0] R, G, B
# self.point.plotPoint(position, color)
3D Viewer
Mouse
- Mouse wheel: if it is rotated forward, the zoom will increase. If it is rotated backwards, it will zoom out.
- Right mouse button: if it is held down and the mouse is dragged, the content of the window will move in the same direction.
- Left mouse button: if it is held down and the mouse is dragged, the content of the window will rotate in the same direction.
Keyboard
- Direction keys and Numerical keypad: the content of the window will move in the same direction of the key.
- Minus keys: if it is held down, it will zoom out.
- Plus keys: if it is held down, the zoom will increase.
Videos
Application Programming Interface
self.getImage('left')- to get the left imageself.getImage('right')- to get the right imageself.point.PlotPoint(position, color)- to plot the point in the 3d tool
Navigating the GUI Interface
Mouse based: Hold and drag to move around the environment. Scroll to zoom in or out
Keyboard based: Arrow keys to move around the environment. W and S keys to zoom in or out
Theory
In computer vision and computer graphics, 3D reconstruction is the process of determining an object’s 3D profile, as well as knowing the 3D coordinate of any point on the profile. Reconstruction can be achieved as follows:
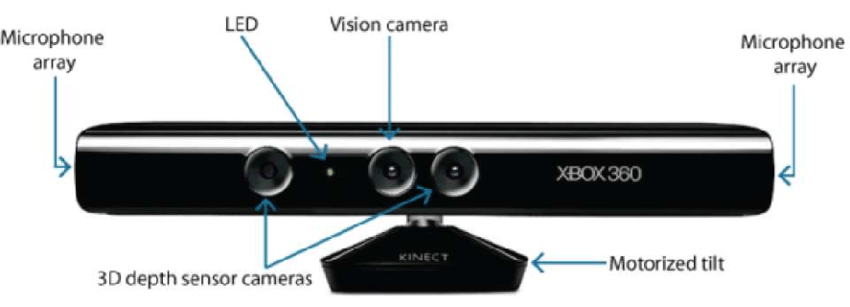
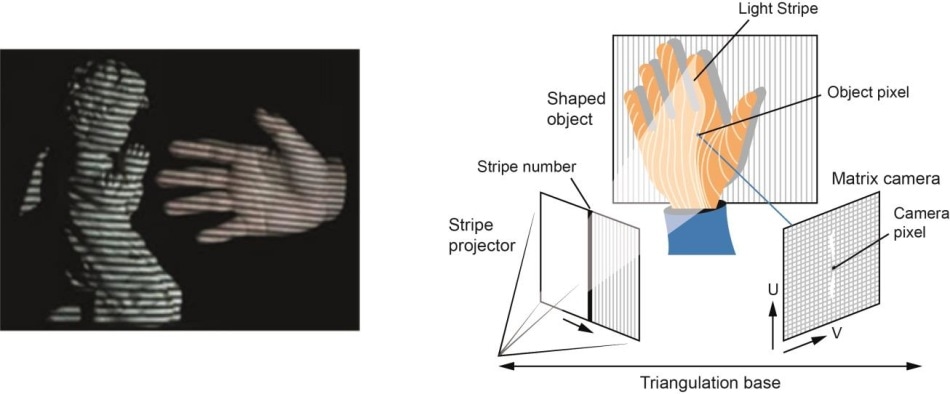
- Hardware Based: Hardware based approach requires us to utilize the hardware specific to the reconstruction task. Use of structured light, laser range finder, depth gauge and radiometric methods are some examples.
- Software Based: Software based approach relies on the computation abilities of the computer to determine the 3D properties of the object. Shape from shading, texture, stereo vision and homography are some good methods.
In this exercise our main aim is to carry out 3d reconstruction using Software based approach, particularly stereo vision 3d reconstruction.
Epipolar Geometry
When two cameras view a 3D scene from two different positions, there are a number of geometric relations between the 3D points and their projections onto the 2D images that lead to constraints between the image points. The study of these properties and constraints is called Epipolar Geometries. The image and explanation below may generalize the idea:

Suppose a point X in 3d space is imaged in two views, at x in the first and x' in the second. Backprojecting the rays to their camera centers through the image planes, we obtain a plane surface, denoted by π.
Supposing now that we know only x, we may ask how the corresponding point x' is constrained. The plane π is determined by the baseline(line connecting the camera centers) and the ray defined by x. From above, we know that the ray corresponding to the unknown point x' lies in π, hence the point x' lies on the line of intersection l' of π with second image plane. This line is called the epipolar line corresponding to x. This relation helps us to reduce the search space of the point in right image, from a plane to a line. Some important definitions to note are:
-
The epipole is the point of intersection of the line joining the camera centers (the baseline) with the image plane.
-
An epipolar plane is a plane containing the baseline.
-
An epipolar line is the intersection of the epipolar plane with the image plane.
Stereo Reconstruction
Stereo reconstruction is a special case of the above 3d reconstruction where the two image planes are parallel to each other and equally distant from the 3d point we want to plot.

In this case the epipolar line for both the image planes are same, and are parallel to the width of the planes, simplifying our constraint better.
3D Reconstruction Algorithm
The reconstruction algorithm consists of 3 steps:
- Detect the feature points in one image plane
- Detect the feature point corresponding the one found above
- Triangulate the point in 3d space
Let’s look at them one by one
Feature Point Detection
Feature Point Detection is a vast area of study where several algorithms are already studied. Harris Corner Detection and Shi-Tomasi algorithms use eigen values to get a good feature point. But, the problem is we need a lot of points for 3D Reconstruction, and these algorithms won’t be able to provide us with such a large number of feature points.
Therefore, we use edge points as our feature points. There may be ambiguity in their detection in the next stage of the algorithm. But, our problem is solved by taking edges as the feature points. One really cool edge detector is Canny Edge Detection Algorithm. The algorithm is quite simple and reliable in terms of generating the edges.
Feature Point Extraction
The use of the epipolar constraint really simplifies the time complexity of our algorithm. For general 3d reconstruction problems, we have to generate an epipolar line for every point in one image frame, and then search in that sample space the corresponding point in the other image frame. The generation of epipolar line is also very easy in our case, it is just the parallel line iterpolation from left image to right image plane.
Checking the correspondence between images involves many algorithms, like Sum of Squared Differences or Energy Minimization. Without going much deep, using a simple Correlation filter also suffices our use case.
Triangulation
Triangulation in simple terms is just calculating where the 3d point is going to lie using the two determined points in the image planes.
In reality, the position of the image points cannot be measured exactly. For general cameras, there may be geometric or physical distortions. Therefore, a lot of mathematics goes behind minimizing that error and calculating the most accurate 3d point projection. Refer to this link for a simple model.
Hints
Simple hints provided to help you solve the 3d_reconstruction exercise. The OpenCV library is used extensively for this exercise.
Setup
Using the exercise API, we can easily retrieve the images. Also, after getting the images, it is a good idea to perform bilateral filtering on the images, because there are some extra details that need not be included during the 3d reconstruction. Check out the illustrations for the effects of performing the bilateral filtering.
Calculating Correspondences
OpenCV already has built-in correlation filters which can be called through matchTemplate(). Take care of extreme cases like edges and corners.
One good observation is that the points on left will have correspondence in the left part and the points on right will have correspondence in the right part. Using this observation, we can easily speed up the calculation of correspondence.
Plotting the Points
Either manual or OpenCV based function triangulatePoints works good for triangulation. Just take care of all the matrix shapes and sizes while carrying out the algebraic implementations.
Keep in mind the difference between simple 3D coordinates and homogenous 4D coordinates. Check out this video for details. Simply dividing the complete 4d vector by its 4th coordinate gives us the 3d coordinates.
Due to varied implementations of users, the user may have to adjust the scale and offset of the triangulated points in order to make them visible and representable in the GUI interface. Downscaling the 3D coordinate vector by a value between 500 to 1000 works well. Also an offset of 0 to 8 works good.
Illustrations


Contributors
- Contributors: Alberto Martín, Francisco Rivas, Francisco Pérez, Jose María Cañas, Nacho Arranz.
- Maintained by Jessica Fernández, Vanessa Fernández and David Valladares.
References
- https://www.researchgate.net/publication/330183516_3D_Computer_Vision_Stereo_and_3D_Reconstruction_from_Disparity
- https://www.iitr.ac.in/departments/MA/uploads/Stereo-updated.pdf
- https://www.cs.auckland.ac.nz/courses/compsci773s1c/lectures/CS773S1C-3DReconstruction.pdf
- https://cs.nyu.edu/~fergus/teaching/vision/9_10_Stereo.pdf
- https://mil.ufl.edu/nechyba/www/eel6562/course_materials/t9.3d_vision/lecture_multiview1x2.pdf
- https://learnopencv.com/introduction-to-epipolar-geometry-and-stereo-vision/
- https://medium.com/@dc.aihub/3d-reconstruction-with-stereo-images-part-1-camera-calibration-d86f750a1ade